Understanding the 100 prisoners problem
I visited my friends Chris and Yuki in Seattle. After lunch, Chris threw us a brainteaser: the 100 prisoners problem. For those not familiar, Minute Physics has a great YouTube video about it.
For those who would prefer not to watch a video, a snippet from the Wikipedia page is attached here:
In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival.
and for some reason that snippet sounds like the voice-over to a movie trailer.
Since we did not have a good intuitive grasp of the solution and reasoning, we decided to simulate the experiment and run some numbers. When in doubt, implement it yourself, right?
The Minute Physics video has 100 boxes, but we should generalize to n.
Since the boxes in the room are shuffled at the beginning of each experiment,
we start by shuffling a list of numbers from 1 to n:
import random
def sample(n=100, limit=50):
boxes = list(range(n))
random.shuffle(boxes)
return sum(try_find_self(boxes, person, limit) for person in range(n))
Then, for each person (which is the same as “for each box” in this case),
attempt to find their hidden box using the method described in the video. Since
try_find_self yields a success (True) or a failure (False), summing
should give the number of people who found their boxes.
def try_find_self(boxes, start, limit):
next_box = boxes[start]
num_opened = 1
while next_box != start and num_opened < limit:
next_box = boxes[next_box]
num_opened += 1
return next_box == start
The try_find_self function implements the strategy described in the video:
start at the box indexed by your number (not necessarily containing your
number) and follow that linked list of boxes until you either hit the limit or
find your number. If the next box at the end is yours, you have found your box!
Now, this isn’t very interesting on its own. We can run an experiment, sure, but we still have to analyze the results of the data over multiple samples and varying parameters.
In order to do that, we made some visualizations. We start off by importing all of the usual suspects:
import random
import simulate
import matplotlib.pyplot as plt
import numpy as np
Then, in order to get reproducible results, seed the random number generator. This was essential for improving our implementations of both the visualizations and the simulations while verifying that the end results did not change.
random.seed(5)
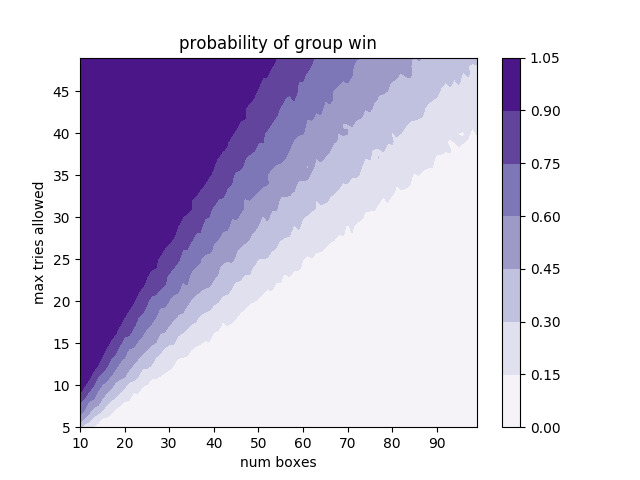
In order to get a feel for the effect of different parameters on the probability of a group of people winning, we varied the number of boxes and the maximum number of tries. It’s a good thing we tried this, since our intuition about how the results scale with the ratio was very wrong.
num_samples = 1000
max_tries_options = np.arange(5, 50, 10)
num_box_options = np.arange(10, 100, 10)
Since our sampler only takes one parameter pair at once, we have to vectorize
our function. Note that we specify otypes, because otherwise vectorize has
to run the sample function with the first input multiple times in order to
determine the type of the output. This is a known issue and
was very annoying to debug, given the randomness.
vsample = np.vectorize(simulate.sample, otypes=[int])
Now we take samples at all combinations of the parameter, num_samples number
of times. This returns a large NumPy array with dimensions like
results[sample_num][max_tries][num_boxes]. For each sample, all of the
combinations of parameters are tried and returned in a 2D grid.
params = np.meshgrid(num_box_options, max_tries_options)
results = np.array([vsample(*params) for _ in range(num_samples)])
This produces some nice data, like this:
[[[10 2 0 ... 1 7 6]
[10 4 30 ... 32 7 1]
[10 20 30 ... 1 11 35]
[10 20 30 ... 70 41 40]
[10 20 30 ... 3 29 30]]
...
[[ 4 13 18 ... 3 2 3]
[10 0 30 ... 31 11 47]
[10 20 30 ... 43 0 34]
[10 20 30 ... 29 80 45]
[10 20 30 ... 70 80 90]]]
While it’s all nice and good to know how many people in each sample found their
boxes, we want to visualize the probability of a group winning. Remember
that a group winning is defined by all of the n people finding their number
in a box. To calculate that probability, we binarize the results and get the
mean success rate across all the samples.
results_bin = np.sum(results == num_box_options, axis=0) / num_samples
This turns the results from above into an array like this:
[[0.337 0.012 0. 0. 0. 0. 0. 0. 0. ]
[1. 0.699 0.338 0.127 0.029 0.007 0.003 0. 0. ]
[1. 1. 0.836 0.545 0.304 0.181 0.072 0.038 0.012]
[1. 1. 1. 0.871 0.662 0.462 0.316 0.197 0.093]
[1. 1. 1. 1. 0.907 0.694 0.54 0.429 0.313]]
which has dimensions results_bin[max_tries][num_boxes].
If you are unfamiliar with the term binarize, I was too until last night. It means reduce to a success/failure value.
There are three interesting regions of this data, identifiable even before plotting:
- The bottom left field of
1s, which comes from allowing many tries compared to the number of boxes in the room. - The top right field of
0s, which comes from allowing not many tries compared to the number of boxes in the room. They really shouldn’t be zero, but winning is so rare that we would need to have a lot of samples. - The middle “normal” numbers.
Let’s chart the data and see what this looks like in beautiful shades of purple:
ax = plt.axes()
plt.set_cmap('Purples')
contour = ax.contourf(*params, results_bin)
ax.set_xlabel('num boxes')
ax.set_ylabel('max tries allowed')
ax.set_title('probability of group win')
plt.colorbar(contour)
plt.show()
Note that this graph was generated with
1000samples, and intervals of1formax_tries_optionsandnum_box_options, which is different than the above code snippets. It took a while to generate the data.
On the x-axis we have the total number of both people and boxes and on the y-axis we have the maximum number of tries that each person is given to find their box. This confirms Minute Physics’ conclusion about the probability of everyone winning using the strategy. It also provides a handy way of testing your own strategy against the proposed one and seeing how often you lead your group to success! Feel free to send any interesting ones in.
If Chris, Yuki, and I have time, we’ll update this post with a more efficient simulation so it doesn’t take so dang long to generate the data. We also have another visualization lying around that contains the different probability distributions for all the configuration settings, but haven’t written about it… yet.
There’s some sample code in the repo — check it out and let us know what you think. We found that re-writing the simulation as a Python C-extension improved speeds 20x, so there’s also a small C++ program in there.